Graph Search

CS314

Review

Previously

  • Control in Prolog, Generate and Test, Programming Lists.

This lecture

  • Graph search
    • Solving a Maze
    • and other problems.

How to reach the center of the maze?

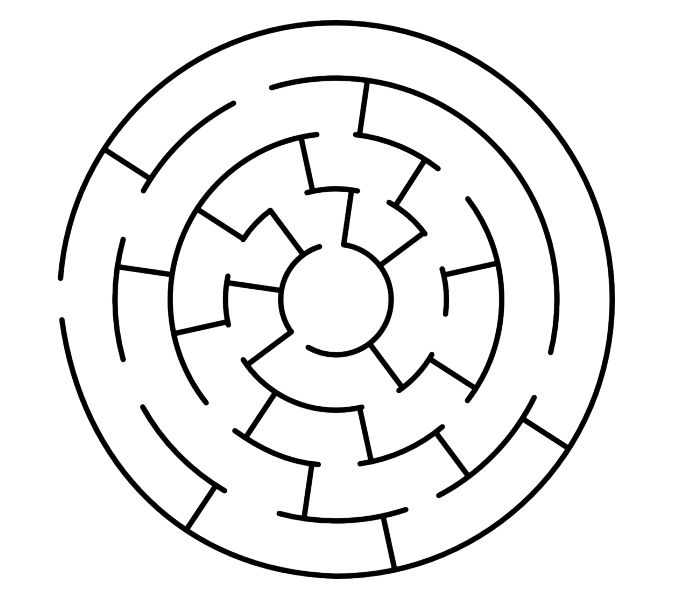
  • There are multiple paths.
    • Only some of the paths may lead to the center.
  • Solving the maze requires graph search.

Learning Goals

  • How to encode this maze as a graph search problem.
  • How to solve this program.
  • How to handle cycles in the search path.

Each opening is a vertex

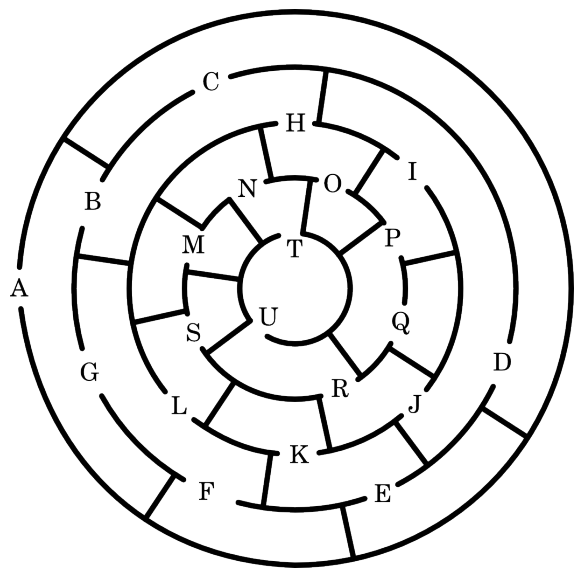
Edges connect adjacent openings

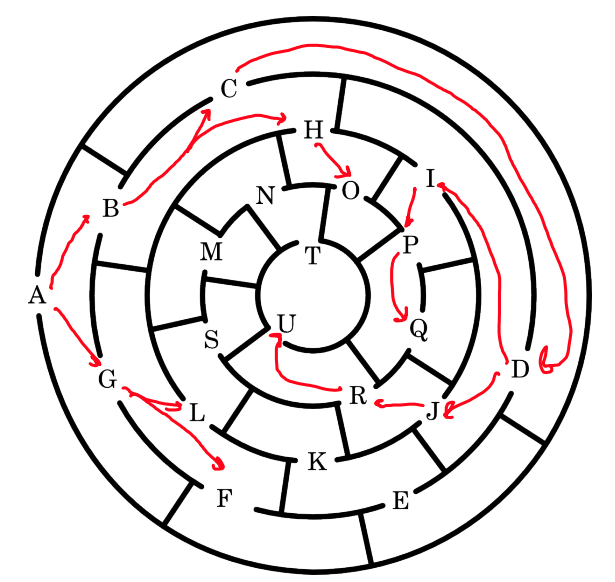
A route(A,B) holds if B is one of the openings reachable on entering through A.

Abstract the maze into a graph.

Encode the graph as facts

In [1]:
route(a,g).
route(a,b).
route(g,l).
route(g,f).
route(l,s).
route(b,c).
route(b,h).
route(c,d).
route(h,o).
route(d,i).
route(d,j).
route(i,p).
route(p,q).
route(j,r).
route(r,u).

Added 15 clauses(s).

Encode the rules for solving the maze

In [2]:
travel(A,A).
travel(A,C) :- route(A,B), travel(B,C).

start(a).
finish(u).

solve :- start(A), finish(B), travel(A,B).

Added 5 clauses(s).
In [3]:
?- solve.

true.

Prolog says that there is a path from a to u.

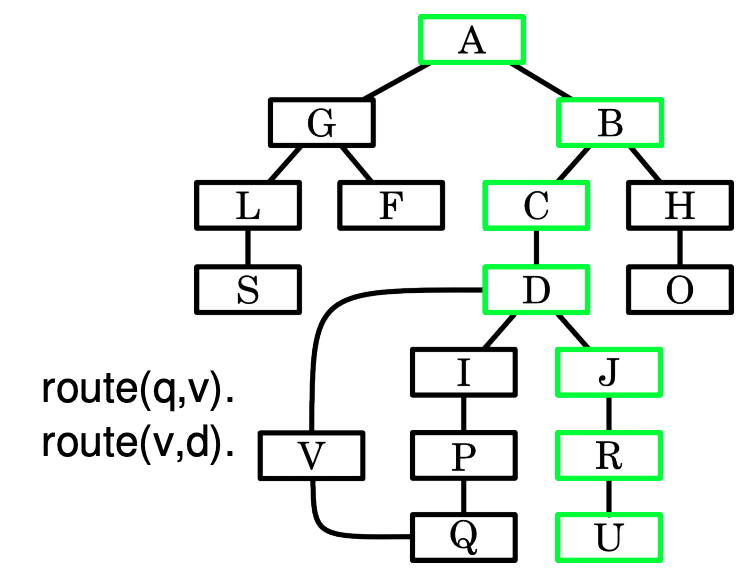
Remembering the route

We can attach a log to remember the travel route.

In [4]:
travellog(A,A,[]).
travellog(A,C,[A-B|Steps]) :-
  route(A,B), travellog(B,C,Steps).
solve(L) :- start(A), finish(B), travellog(A,B,L).

Added 3 clauses(s).
In [5]:
?- solve(L).

L = [ a-b, b-c, c-d, d-j, j-r, r-u ] .

What if there are cycles in the graph

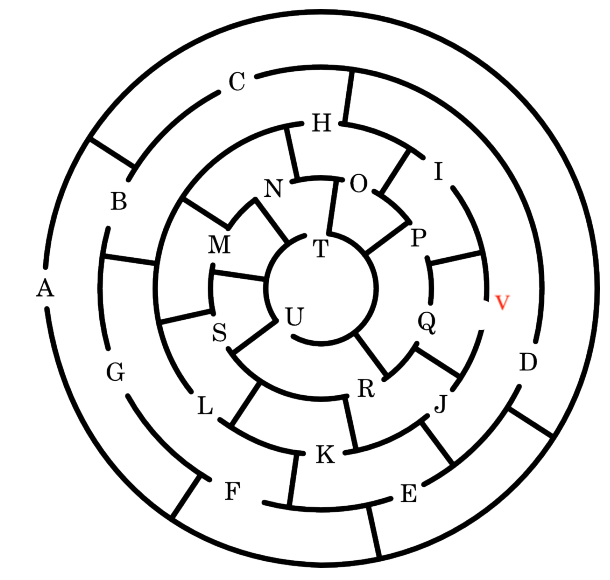
  • Prolog does DFS
  • Search can go into an infinite loop a-b-c-d-v-q-p-i-v-q-p-i-v-....

Cyclic graph

Cyclic graph

In [6]:
route(q,v).
route(v,d).

Added 2 clauses(s).
In [ ]:
?- solve.

goes into an infinite loop.

Remembering visited nodes

In [7]:
travelsafe(A,A,_).
travelsafe(A,C,Visited) :-
  route(A,B),
  not(member(B,Visited)), 
  travelsafe(B,C,[B|Visited]).

Added 2 clauses(s).
In [8]:
solve2 :- start(A), finish(B), travelsafe(A,B,[A]).

Added 1 clauses(s).
In [9]:
?- solve2.

true.

Exercise: Implement solve2 with a log.

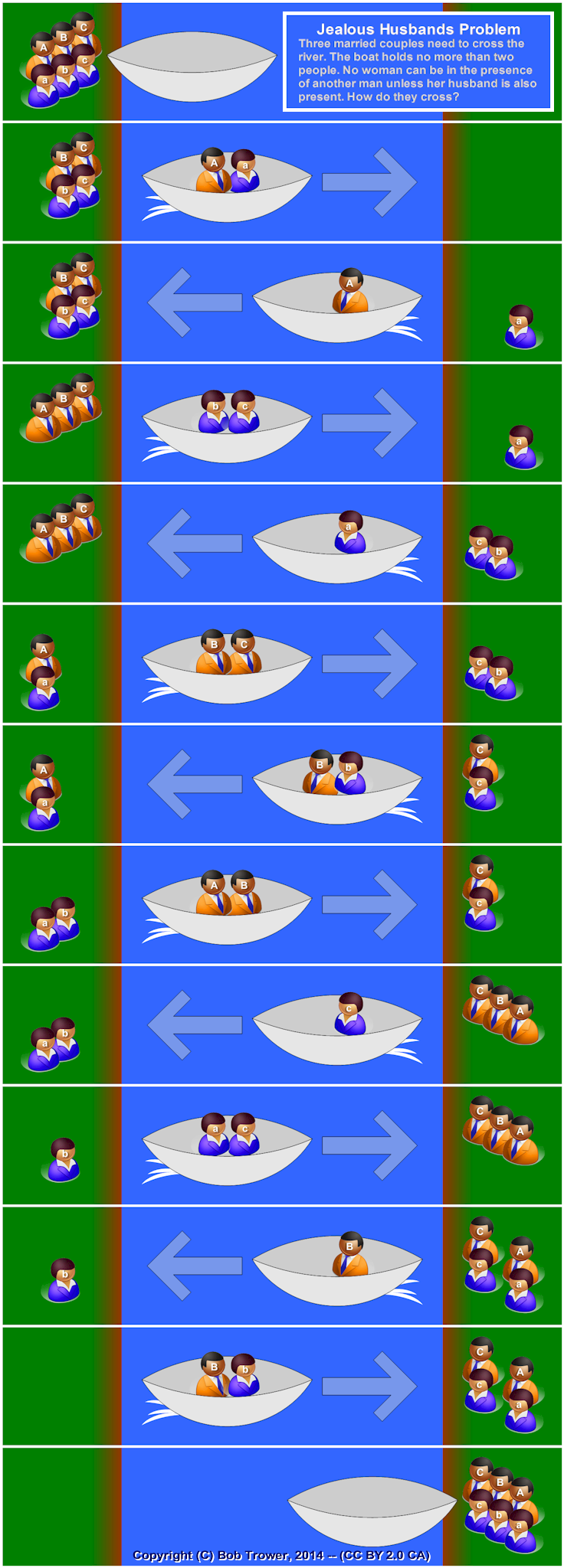
Missionaries and Cannibals

Maze is quite straight-forward to map. Other problems not so much.

  • 3 missionaries, 3 cannibals and 1 boat.
  • The boat carries 2 people.
  • If the Cannibals outnumber the Missionaries they will eat them.
  • Get them all from one side of the river to the other?

Represent the state

We need to represent the number of missionaries and cannibals on each bank, and where the boat is.

In [10]:
start(3-3-0-0-l).
finish(0-0-3-3-_).

Added 2 clauses(s).

Check for safety of a state

A state is safe if no missionary gets eaten.

A missionary gets eaten if there is at least one missonary on a bank and the number of cannibals on that bank outnumber them.

In [11]:
safe(0-_-M2-C2-_) :- M2 >= C2.
safe(M1-C1-0-_-_) :- M1 >= C1.
safe(M1-C1-M2-C2-_) :- M1 >= C1, M2 >= C2.

Added 3 clauses(s).

Defining steps

In order to define a transition, we need all possible ways we can take a step. The boat can carry at most 2 people and at least one person.

In [12]:
carry(2,0).
carry(1,1).
carry(0,2).
carry(1,0).
carry(0,1).

Added 5 clauses(s).

Defining transitions

A predicate step(A,B) is defined if there is a carry/2 that moves the state from A to B.

State M1-C1-M2-C2-l means M1 missionaries and C1 cannibals on the left bank, M2 missionaries and C2 cannibals on the right bank, and the boat is besides the left bank.

State M3-C3-M4-C4-r means M3 missionaries and C3 cannibals on the left bank, M4 missionaries and C4 cannibals on the right bank, and the boat is besides the right bank.

Defining transitions

A predicate step(A,B) is defined if there is a carry/2 that moves the state from A to B.

In [13]:
step(M1-C1-M2-C2-l,M3-C3-M4-C4-r) :-
  carry(X,Y),
  M1 >= X, M3 is M1 - X, M4 is M2+X,
  C1 >= Y, C3 is C1 - Y, C4 is C2+Y.
  
step(M1-C1-M2-C2-r,M3-C3-M4-C4-l) :-
  carry(X,Y),
  M2 >= X, M4 is M2 - X, M3 is M1+X,
  C2 >= Y, C4 is C2 - Y, C3 is C1+Y.

Added 2 clauses(s).
  • Observe that there may be multiple possible target transition for a source transition.
  • Each such possible transition is an outedge in the game graph.

Defining the game

We need to define the game as a series of steps, where each step is safe and we do not visit the same steps again.

We use Visited list to track visited states and maintain a log of steps.

In [14]:
travel(A,A,_,[]).
travel(A,C,Visited,[B|Steps]) :- 
  step(A,B), safe(B), not(member(B,Visited)), travel(B,C,[A,B|Visited],Steps).

Added 2 clauses(s).

Solving the game

Solution to the same is a series steps that go from initial to final state.

In [15]:
solve3(L) :- start(A), finish(B), travel(A,B,[],L).

Added 1 clauses(s).
In [16]:
?- solve3(L) {1}.

L = [ -(-(-(2, 2), 1), 1)-r, -(-(-(3, 2), 0), 1)-l, -(-(-(3, 0), 0), 3)-r, -(-(-(3, 1), 0), 2)-l, -(-(-(1, 1), 2), 2)-r, -(-(-(2, 2), 1), 1)-l, -(-(-(0, 2), 3), 1)-r, -(-(-(0, 3), 3), 0)-l, -(-(-(0, 1), 3), 2)-r, -(-(-(1, 1), 2), 2)-l, -(-(-(0, 0), 3), 3)-r ] .

Solving the game

The solution is the same is what is illustrated here:

Exercise: Towers of Hanoi