Generate and Test

CS314

Review

Previously

  • Programming with Lists

This lecture

  • Generate and Test
    • Design pattern for programming with Prolog
    • Solve some more puzzles by applying our knowledge of backtracking and choice points

Take from a list

take(HasX,X,NoX) removes exactly one element X from the list HasX with the result list being NoX.

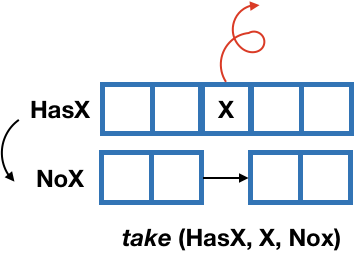
take(HasX,X,NoX) removes exactly one element X from the list HasX with the result list being NoX.

In [1]:
take([H|T],H,T).
take([H|T],R,[H|S]) :- take(T,R,S).

Added 2 clauses(s).

Read the second clause as, "Given a list [H|T] you can take R from the list and leave [H|S] if you can take R from T and leave S".

Take from a list

In [2]:
?- take([1,2,3],1, Y).

Y = [ 2, 3 ] .
In [3]:
?- take([2,3],1,X).

false.
In [4]:
?- take([1,2,3],X,Y).

Y = [ 2, 3 ], X = 1 ;
Y = [ 1, 3 ], X = 2 ;
Y = [ 1, 2 ], X = 3 .

Permutation

We can now build permutation using take.

In [5]:
perm([],[]).
perm(L,[H|T]) :- take(L,H,R), perm(R,T).

Added 2 clauses(s).
In [6]:
?- perm([1,2,3],X).

X = [ 1, 2, 3 ] ;
X = [ 1, 3, 2 ] ;
X = [ 2, 1, 3 ] ;
X = [ 2, 3, 1 ] ;
X = [ 3, 1, 2 ] ;
X = [ 3, 2, 1 ] .

Generate and test

  • A design pattern for logic programming.
  • Generate a candidate solution and then test if the solution satisfies the condition.

Dutch national flag

dutch flag
  • A famous problem formulated by Edsger Dijkstra.
  • Given a list with colours red, white and blue, return a list such that it has all the reds, and then white followed by blue.
    • Essentially a sorting problem.

Dutch national flag

Implement a predicate checkFlag(L) to see whether the list L contains the colours in the right order.

In [7]:
checkRed([red|T]) :- checkRed(T).
checkRed([white|T]) :- checkWhite(T).
checkWhite([white|T]) :- checkWhite(T).
checkWhite([blue|T]) :- checkBlue(T).
checkBlue([blue|T]) :- checkBlue(T).
checkBlue([]).
checkFlag(L) :- checkRed(L).

Added 7 clauses(s).
In [8]:
?- checkFlag([red,white,blue,blue]).

true.
In [9]:
?- checkFlag([white,red,blue,blue]).

false.

Quiz

checkRed([red|T]) :- checkRed(T).
checkRed([white|T]) :- checkWhite(T).
checkWhite([white|T]) :- checkWhite(T).
checkWhite([blue|T]) :- checkBlue(T).
checkBlue([blue|T]) :- checkBlue(T).
checkBlue([]).
checkFlag(L) :- checkRed(L).

Which one of the following queries is true?

  1. ?- checkFlag([white,blue]).
  2. ?- checkFlag([blue]).
  3. ?- checkFlag([]).

Quiz

Which one of the following queries is true?

  1. ?- checkFlag([white,blue]). true
  2. ?- checkFlag([blue]). false
  3. ?- checkFlag([]). false

How can we prevent the first predicate from holding?

Better flag check

Introduce a new state chkRed2 in the transition system.

In [10]:
chkRed([red|T]) :- chkRed2(T).
chkRed2([red|T]) :- chkRed2(T).
chkRed2([white|T]) :- chkWhite(T).
chkWhite([white|T]) :- chkWhite(T).
chkWhite([blue|T]) :- chkBlue(T).
chkBlue([blue|T]) :- chkBlue(T).
chkBlue([]).
chkFlag(L) :- chkRed(L).

Added 8 clauses(s).
In [11]:
?- chkFlag([white,blue]).

false.

Make the dutch national flag

Using the predicate mkFlag(L,F) which makes the flag F from the list of colours in L.

In [12]:
mkFlag(L,F) :- perm(L,F), chkFlag(F).

Added 1 clauses(s).
In [13]:
?- mkFlag([white,red,blue,blue,blue],F) {1}.

F = [ red, white, blue, blue, blue ] .

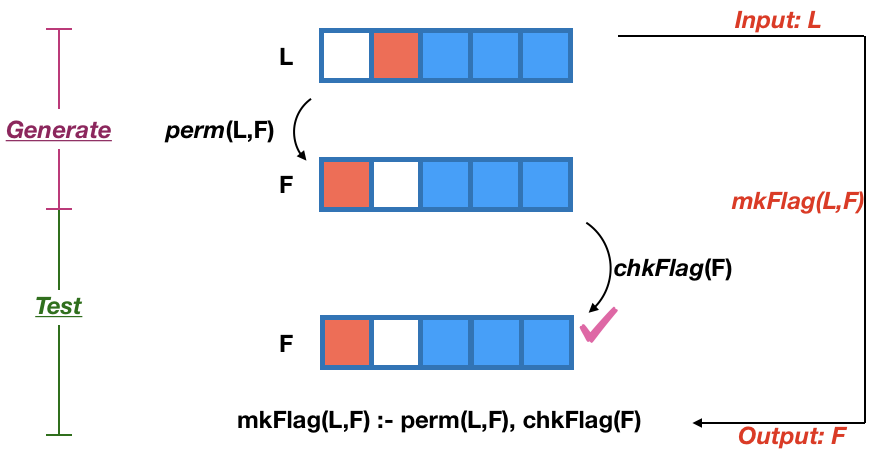
In the above, perm is the generate and chkFlag is the test.

Essence of generate and test

  1. Generate a solution.
  2. Test if it is valid.
  3. If not valid, backtrack and try another solution.

Sorting

We can generalise our solution to the Dutch national flag problem to sorting.

Let us define a predicate sorted(L) which holds if L is sorted.

In [14]:
sorted([]).
sorted([H]).
sorted([A,B|T]) :- A =< B, sorted([B|T]).

Added 3 clauses(s).
In [15]:
?- sorted([1,2,3,4]).

true.
In [16]:
?- sorted([1,3,2,4]).

false.

Sorting

Now sorting can be defined using the predicate permsort(L,SL), where SL is the sorted version of L.

In [17]:
permsort(L,SL) :- perm(L,SL), sorted(SL).

Added 1 clauses(s).
In [18]:
?- permsort([1,3,5,2,4,6], SL).

SL = [ 1, 2, 3, 4, 5, 6 ] .
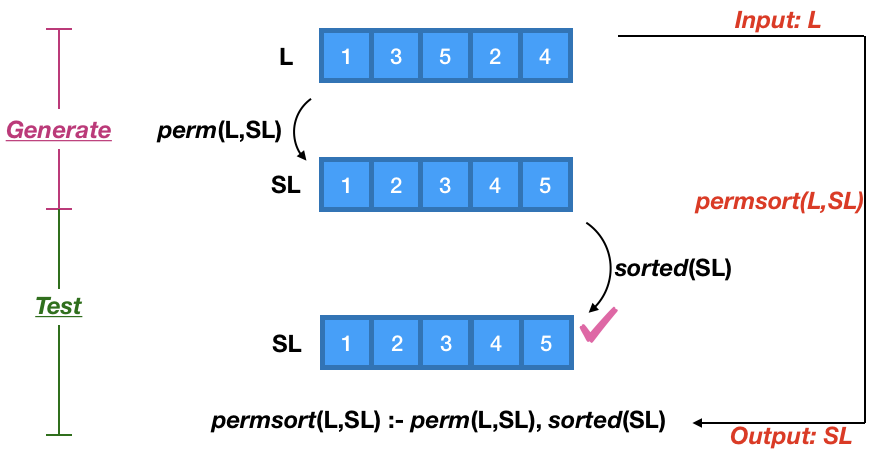
  • Generating all the permutations and checking for sortedness is a terrible idea.
  • A better approach is to divide and conquer.

Quicksort

  • A bit of a digression from generate and test.
  • Use divide and conquer to sort the results.
  • First, define the predicate partition(L,X,LES,GS) that given a list L and an element X partitions the list into two.
    • The first is LES which contains elements from L less than or equal to X and
    • GS which contains elements from L greater than X.

Quicksort

Let's first define a partition predicate partition(Xs,X,Ls,Rs) that partitions elements in Xs into Ls and Rs where $\forall E \in Ls. E =< X$ and $\forall E \in Rs. E > X$.

In [19]:
partition([],Y,[],[]).
partition([X|Xs],Y,[X|Ls],Rs) :- X =< Y, partition(Xs,Y,Ls,Rs).
partition([X|Xs],Y,Ls,[X|Rs]) :- X > Y, partition(Xs,Y,Ls,Rs).

Added 3 clauses(s).
In [20]:
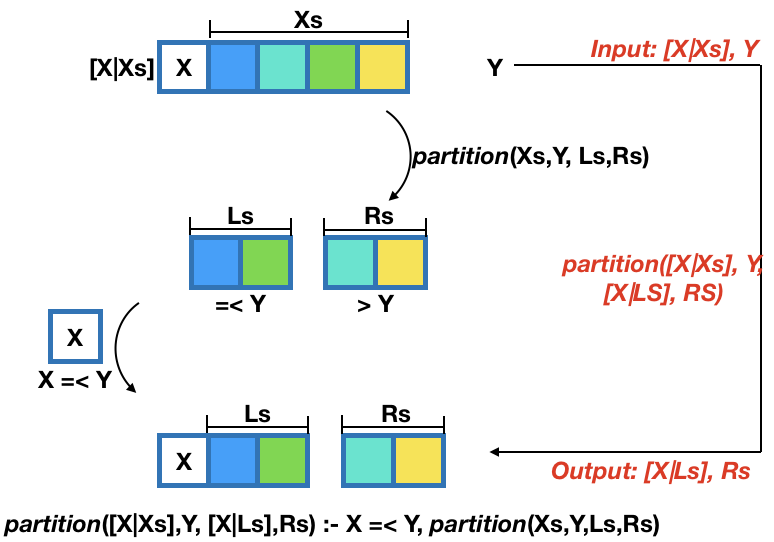
?- partition([6,5,3,2,1,0],4,X,Y).

Y = [ 6, 5 ], X = [ 3, 2, 1, 0 ] .

Quicksort

Quicksort works by partitioning the list into two, sorting each one, and appending to get the resultant sorted list.

In [21]:
quicksort([H|T],SL) :-
  partition(T,H,Ls,Rs), quicksort(Ls,SLs), quicksort(Rs,SRs), append(SLs,[H|SRs],SL).
quicksort([],[]).

Added 2 clauses(s).
In [22]:
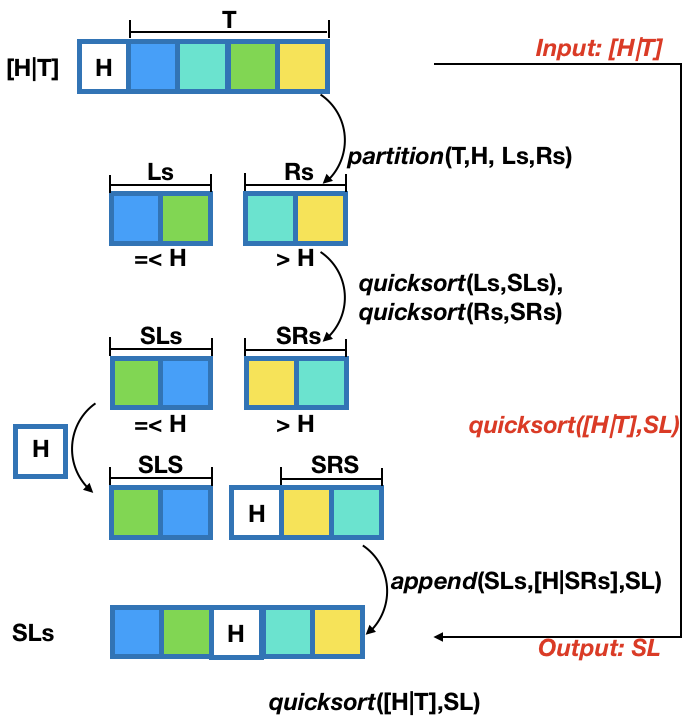
?- quicksort([6,5,4,3,2,1,0],SL).

SL = [ 0, 1, 2, 3, 4, 5, 6 ] .

N-Queens problem

Find the assignment of N-queens on a NxN chessboard such that none of the queens threaten each other.

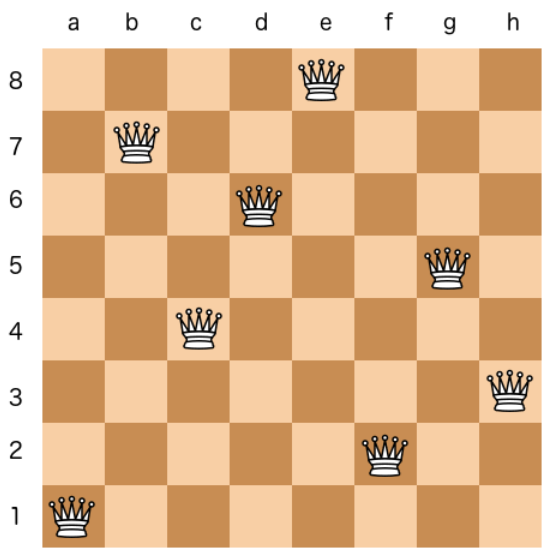
The problem of finding all solutions even to the 8-queens problem can be quite computationally expensive, as there are 4,426,165,368 possible arrangements of eight queens on an 8×8 board, but only 92 solutions.

N-Queens Problem

  • If two queens are on the same row or same column, they threaten each other.
    • So design the data structure such that such cases are ruled out.
  • Represent the positions of the queens as a permutation of [1,2,3,...,N].
    • Each number represents the position of the queen in that row.
    • [1,6,8,3,7,4,2,5] says that the first queen is on (1,1), second on (2,6), thrid on (3,8), forth on (4,3), fifith on (5,7), ...
    • The soution, if it exists, is a permutation of [1,2,3,...,N].

  • Represent the positions of the queens as a permutation of [1,2,3,...,N].

    • Each number represents the position of the queen in that row.
    • [1,6,8,3,7,4,2,5] says that the first queen is on (1,1), second on (2,6), thrid on (3,8), forth on (4,3), fifith on (5,7), ...
    • The soution, if it exists, is a permutation of [1,2,3,...,N].

  • Importantly, two queens cannot be on the same row or column.

    • No need to check for this condition while checking validity.
    • Such permutations aren't even generated, making the search fast.

N-Queens problem

In [23]:
checkBoard([H|T]) :- L is H-1, R is H+1, checkRow(T,L,R), checkBoard(T).
checkRow([H|T],L,R) :- H =\= L, H =\= R, LN is L-1, RN is R+1, checkRow(T,LN,RN).
checkBoard([]).
checkRow([],_,_).

Added 4 clauses(s).

Example:

8-Queens Problem

In [24]:
?- checkBoard([1,6,8,3,7,4,2,5]).

true.
In [25]:
queens(B) :- perm([ 1, 2, 3, 4, 5, 6, 7, 8 ], B), checkBoard(B).

Added 1 clauses(s).
In [26]:
?- queens(B) {1}.

B = [ 1, 5, 8, 6, 3, 7, 2, 4 ] .

8-queens Problem

There are 92 solutions to 8-Queens problem. We can find them all.

In [27]:
?- queens(B) {92}.

B = [ 1, 5, 8, 6, 3, 7, 2, 4 ] ;
B = [ 1, 6, 8, 3, 7, 4, 2, 5 ] ;
B = [ 1, 7, 4, 6, 8, 2, 5, 3 ] ;
B = [ 1, 7, 5, 8, 2, 4, 6, 3 ] ;
B = [ 2, 4, 6, 8, 3, 1, 7, 5 ] ;
B = [ 2, 5, 7, 1, 3, 8, 6, 4 ] ;
B = [ 2, 5, 7, 4, 1, 8, 6, 3 ] ;
B = [ 2, 6, 1, 7, 4, 8, 3, 5 ] ;
B = [ 2, 6, 8, 3, 1, 4, 7, 5 ] ;
B = [ 2, 7, 3, 6, 8, 5, 1, 4 ] ;
B = [ 2, 7, 5, 8, 1, 4, 6, 3 ] ;
B = [ 2, 8, 6, 1, 3, 5, 7, 4 ] ;
B = [ 3, 1, 7, 5, 8, 2, 4, 6 ] ;
B = [ 3, 5, 2, 8, 1, 7, 4, 6 ] ;
B = [ 3, 5, 2, 8, 6, 4, 7, 1 ] ;
B = [ 3, 5, 7, 1, 4, 2, 8, 6 ] ;
B = [ 3, 5, 8, 4, 1, 7, 2, 6 ] ;
B = [ 3, 6, 2, 5, 8, 1, 7, 4 ] ;
B = [ 3, 6, 2, 7, 1, 4, 8, 5 ] ;
B = [ 3, 6, 2, 7, 5, 1, 8, 4 ] ;
B = [ 3, 6, 4, 1, 8, 5, 7, 2 ] ;
B = [ 3, 6, 4, 2, 8, 5, 7, 1 ] ;
B = [ 3, 6, 8, 1, 4, 7, 5, 2 ] ;
B = [ 3, 6, 8, 1, 5, 7, 2, 4 ] ;
B = [ 3, 6, 8, 2, 4, 1, 7, 5 ] ;
B = [ 3, 7, 2, 8, 5, 1, 4, 6 ] ;
B = [ 3, 7, 2, 8, 6, 4, 1, 5 ] ;
B = [ 3, 8, 4, 7, 1, 6, 2, 5 ] ;
B = [ 4, 1, 5, 8, 2, 7, 3, 6 ] ;
B = [ 4, 1, 5, 8, 6, 3, 7, 2 ] ;
B = [ 4, 2, 5, 8, 6, 1, 3, 7 ] ;
B = [ 4, 2, 7, 3, 6, 8, 1, 5 ] ;
B = [ 4, 2, 7, 3, 6, 8, 5, 1 ] ;
B = [ 4, 2, 7, 5, 1, 8, 6, 3 ] ;
B = [ 4, 2, 8, 5, 7, 1, 3, 6 ] ;
B = [ 4, 2, 8, 6, 1, 3, 5, 7 ] ;
B = [ 4, 6, 1, 5, 2, 8, 3, 7 ] ;
B = [ 4, 6, 8, 2, 7, 1, 3, 5 ] ;
B = [ 4, 6, 8, 3, 1, 7, 5, 2 ] ;
B = [ 4, 7, 1, 8, 5, 2, 6, 3 ] ;
B = [ 4, 7, 3, 8, 2, 5, 1, 6 ] ;
B = [ 4, 7, 5, 2, 6, 1, 3, 8 ] ;
B = [ 4, 7, 5, 3, 1, 6, 8, 2 ] ;
B = [ 4, 8, 1, 3, 6, 2, 7, 5 ] ;
B = [ 4, 8, 1, 5, 7, 2, 6, 3 ] ;
B = [ 4, 8, 5, 3, 1, 7, 2, 6 ] ;
B = [ 5, 1, 4, 6, 8, 2, 7, 3 ] ;
B = [ 5, 1, 8, 4, 2, 7, 3, 6 ] ;
B = [ 5, 1, 8, 6, 3, 7, 2, 4 ] ;
B = [ 5, 2, 4, 6, 8, 3, 1, 7 ] ;
B = [ 5, 2, 4, 7, 3, 8, 6, 1 ] ;
B = [ 5, 2, 6, 1, 7, 4, 8, 3 ] ;
B = [ 5, 2, 8, 1, 4, 7, 3, 6 ] ;
B = [ 5, 3, 1, 6, 8, 2, 4, 7 ] ;
B = [ 5, 3, 1, 7, 2, 8, 6, 4 ] ;
B = [ 5, 3, 8, 4, 7, 1, 6, 2 ] ;
B = [ 5, 7, 1, 3, 8, 6, 4, 2 ] ;
B = [ 5, 7, 1, 4, 2, 8, 6, 3 ] ;
B = [ 5, 7, 2, 4, 8, 1, 3, 6 ] ;
B = [ 5, 7, 2, 6, 3, 1, 4, 8 ] ;
B = [ 5, 7, 2, 6, 3, 1, 8, 4 ] ;
B = [ 5, 7, 4, 1, 3, 8, 6, 2 ] ;
B = [ 5, 8, 4, 1, 3, 6, 2, 7 ] ;
B = [ 5, 8, 4, 1, 7, 2, 6, 3 ] ;
B = [ 6, 1, 5, 2, 8, 3, 7, 4 ] ;
B = [ 6, 2, 7, 1, 3, 5, 8, 4 ] ;
B = [ 6, 2, 7, 1, 4, 8, 5, 3 ] ;
B = [ 6, 3, 1, 7, 5, 8, 2, 4 ] ;
B = [ 6, 3, 1, 8, 4, 2, 7, 5 ] ;
B = [ 6, 3, 1, 8, 5, 2, 4, 7 ] ;
B = [ 6, 3, 5, 7, 1, 4, 2, 8 ] ;
B = [ 6, 3, 5, 8, 1, 4, 2, 7 ] ;
B = [ 6, 3, 7, 2, 4, 8, 1, 5 ] ;
B = [ 6, 3, 7, 2, 8, 5, 1, 4 ] ;
B = [ 6, 3, 7, 4, 1, 8, 2, 5 ] ;
B = [ 6, 4, 1, 5, 8, 2, 7, 3 ] ;
B = [ 6, 4, 2, 8, 5, 7, 1, 3 ] ;
B = [ 6, 4, 7, 1, 3, 5, 2, 8 ] ;
B = [ 6, 4, 7, 1, 8, 2, 5, 3 ] ;
B = [ 6, 8, 2, 4, 1, 7, 5, 3 ] ;
B = [ 7, 1, 3, 8, 6, 4, 2, 5 ] ;
B = [ 7, 2, 4, 1, 8, 5, 3, 6 ] ;
B = [ 7, 2, 6, 3, 1, 4, 8, 5 ] ;
B = [ 7, 3, 1, 6, 8, 5, 2, 4 ] ;
B = [ 7, 3, 8, 2, 5, 1, 6, 4 ] ;
B = [ 7, 4, 2, 5, 8, 1, 3, 6 ] ;
B = [ 7, 4, 2, 8, 6, 1, 3, 5 ] ;
B = [ 7, 5, 3, 1, 6, 8, 2, 4 ] ;
B = [ 8, 2, 4, 1, 7, 5, 3, 6 ] ;
B = [ 8, 2, 5, 3, 1, 7, 4, 6 ] ;
B = [ 8, 3, 1, 6, 2, 5, 7, 4 ] ;
B = [ 8, 4, 1, 3, 6, 2, 7, 5 ] .