Control in Prolog

CS314

Review

Previously

  • Programming with Lists, Arithmetic, Backtracking, Choice Points, Generate and Test

This lecture

  • Control in Prolog
    • Rule/fact Order, Goal Order
    • An abstract interpreter for logic programs
      • Unification, Substitution

Algorithm = Logic + Control

  • Logic: facts, rules and goals (queries)
  • Control: how prolog chooses the rules/facts and goals, among several available options.

Main control decisions: Rule/Fact Order and Goal Order.

Rules/Facts

Goals

Algorithm = Logic + Control

  • Rule/fact order: Given a program with a collection of facts and rules, in which order do you choose to pick a rule/fact to unify.

    • SWI-Prolog chooses the first applicable rule in the order in which they appear in the program.

  • Goal order: Given a set of goals in a query to resolve, which goal do you choose

    • SWI-Prolog: chooses the left-most sub-goal.

Rule/fact order and goal order influence program behaviour.

Substring in Prolog

<-------X-------->
+-------------------------------+
|      |    S    |              |  
+-------------------------------+
<--------------Z---------------->

prefix X of Z and suffix S of X.

The corresponding prolog rules are:

In [1]:
append([],Q,Q).
append([H | P], Q, [H | R]) :- append(P, Q, R).
prefix(X,Z) :- append(X,Y,Z).
suffix(Y,Z) :- append(X,Y,Z).

Added 4 clauses(s).

Does goal order change solutions?

Usually produce the same result:

In [2]:
?- prefix(S,[a,b,c,d]), suffix(S,[a,b,c]).

S = [  ] ;
S = [ a, b, c ] .
In [3]:
?- suffix(S,[a,b,c]), prefix(S,[a,b,c,d]).

S = [ a, b, c ] ;
S = [  ] .

Goal order changes solutions

Their answers however differ in other cases:

In [4]:
?- prefix(X,[b]), suffix([a],X).

false.
In [5]:
?- suffix([a],X), prefix(X,[b]).

ERROR: Caused by: '  suffix([a],X), prefix(X,[b])'. Returned: 'error(resource_error(stack), Atom('24453')(stack_overflow, 1, choicepoints, 23646827, depth, 4, environments, 738963, globalused, 0, localused, [Functor(532877,3,23646827,:(user, append(_94, [1], _98)),[]), Functor(532877,3,2,:(system, <meta-call>(<garbage_collected>)),[]), Functor(532877,3,1,:(user, pyrun(<garbage_collected>, [1])),[]), Functor(532877,3,0,:(system, $c_call_prolog),[])], stack, 1048576, stack_limit, 0, trailused))'.

Rule order affects the search for solutions

Recall the definition append.

In [6]:
append([],Q,Q).
append([H | P], Q, [H | R]) :- append(P, Q, R).





















Consider the definition appen2 which reorders the rules from append.













In [7]:



    


appen2([H | P], Q, [H | R]) :- appen2(P, Q, R).
appen2([],Q,Q).



    















    






Added 2 clauses(s).




















Rule order affects the search for solutions
Consider the query:













In [8]:



    


?- append(X,[c],Z) {5}.



    















    






X = [  ], Z = [ c ] ;
X = [ _224 ], Z = [ _224, c ] ;
X = [ _224, _236 ], Z = [ _224, _236, c ] ;
X = [ _224, _236, _248 ], Z = [ _224, _236, _248, c ] ;
X = [ _224, _236, _248, _260 ], Z = [ _224, _236, _248, _260, c ] .


















In [9]:



    


?- appen2(X,[c],Z) {1}.



    















    






ERROR: Caused by: '  appen2(X,[c],Z) '. Returned: 'error(resource_error(stack), Atom('24453')(stack_overflow, 4194188, choicepoints, 4194189, depth, 4194190, environments, 196602, globalused, 753643, localused, [Functor(532877,3,4194189,:(user, appen2(_80, [1], _84)),[]), Functor(532877,3,4194188,:(user, appen2([1], [1], [1])),[])], non_terminating, 1048576, stack_limit, 65534, trailused))'.





































Abstract interpreter for logic programs
We can precisely define the influence of rule orders and goal orders by describing an abstract interpreter for logic programs.


First, we will start off with some definitions of ideas that we have informally seen earlier.















Substitution
A substitution is a finite set of pairs of terms $\{X_1/t_1, \ldots, X_n/t_n\}$ where each $t_i$ is a term and each $X_i$ is a variable such that $X_i \neq t_i$ and $X_i \neq X_j$ if $i \neq j$.


The empty substitution is denoted by $\epsilon$.


For example, $\sigma = \{X/[1,2,3], Y/Z, Z/f(a,b)\}$ is substitution.















Quiz
Is this a valid substitution?

$$
\{X/Y,Y/X,Z/Z,A/a1,A/a2,m/n\}
$$













Quiz
Is this a valid substitution?

$$
\sigma = \{X/Y,Y/X,Z/Z,A/a1,A/a2,m/n\}
$$
No.


    

  • $Z/Z$ should not be in $\sigma$.
    • 

  • Variable $A$ has two substitutions $A/a1$ and $A/a2$, which is incorrect.
    • 

  • $m/n$ is not a valid substitution; $m$ should be a variable.
    • 

  • $X/Y,Y/X \in \sigma$ is fine. 
    • 
















Application of substitution
The application of substitution $\sigma$ to a variable $X$, written as $X\sigma$ is defined

$$
X\sigma = 
\begin{cases}
t \text{ if } X/t \in \sigma \\
X \text{ otherwise}
\end{cases}
$$













Application of substitution
Let $\sigma$ be a substitution $\{X_1/t_1, \ldots, X_n/t_n\}$ and $E$ a term or a formula. The application $E\sigma$ of $\sigma$ to $E$ is obtained by simultaneously replacing every occurrence of $X_i$ in E with $t_i$.


Given $\sigma = \{X/[1,2,3], Y/Z, Z/f(a,b)\}$ and $E = f(X,Y,Z)$, $E\sigma = f([1,2,3],Z,f(a,b))$.


Now, $E\sigma$ is known as an instance of $E$.















Unification
At the core of how Prolog computes is Unification, which is based on Substitution.


There are 3 rules for unification:


    

  • Atoms unify if they are identical
      

    • e.g., monday & monday unifty but not monday & wednesday.
      • 

    

    • 

  • Variables unify with anything.
      

    • e.g., X & monday unify, X & black (friday).
      • 

    

    • 

  • Compound terms unfiy only if their top-function symbols and arities match and their arguments unify recursively.
      

    • e.g., black(X) & black(friday) unify, next(thursday, Y) & next(thursday, friday) unify, play(sunday) & study(X) do not unify.
      • 

    

    • 
















Quiz
Which of these unify?


    

  1. a & a    
    2. 

  2. a & b
    3. 

  3. a & A
    4. 

  4. a & B
    5. 

  5. tree(l,r) & A
    6. 
















Quiz
Which of these unify?


    

  1. a & a yes    
    2. 

  2. a & b no
    3. 

  3. a & A yes
    4. 

  4. a & B yes
    5. 

  5. tree(l,r) & A yes
    6. 
















Quiz
Which of these unify?


    

  1. tree(l,r) & tree(B,C)
    2. 

  2. tree(A,r) & tree(l,C)
    3. 

  3. tree(A,r) & tree(A,B)
    4. 

  4. A & a(A)
    5. 

  5. a & a(A)
    6. 
















Quiz
Which of these unify?


    

  1. tree(l,r) & tree(B,C) yes
    2. 

  2. tree(A,r) & tree(l,C) yes
    3. 

  3. tree(A,r) & tree(A,B) yes
    4. 

  4. A & a(A) yes (mostly), occurs check disabled by default
    5. 

  5. a & a(A) no
    6. 
















Unifer
Let $S$ and $T$ be two terms. A substitution $\sigma$ is a unfier for $S$ and $T$ if $S\sigma$ and $T\sigma$ are syntactically equal.


Let $S = f(X,Y)$ and $T = f(g(Z),Z)$. Let $\sigma = \{X/g(Z), Y/Z\}$. $\sigma$ is a unfier for $S$ and $T$.















More than one unifier
A pair of terms may have more than one unifier. For example, for the terms $f(X,X)$ and $f(Y,Z)$, the unifiers $\theta = \{X/Y,Z/Y\}$ and $\sigma = \{X/Z,Y/Z\}$ are both unifiers.















Quiz
What is a unifier of $f(P,P,Q)$ and $f(Q,R,a)$


    

  1. $\{P/a,Q/a,R/a\}$
    2. 

  2. $\{P/b,Q/b,R/b\}$
    3. 

  3. $\{P/Q,R/Q\}$
    4. 

  4. $\epsilon$
    5. 
















Quiz
What is a unifier of $f(P,P,Q)$ and $f(Q,R,a)$


    

  1. $\{P/a,Q/a,R/a\}$ ✓
    2. 

  2. $\{P/b,Q/b,R/b\}$
    3. 

  3. $\{P/Q,R/Q\}$
    4. 

  4. $\epsilon$
    5. 
















Recursive Side-effect free algorithm for computing a unifier
Input: Two terms $X$ and $Y$ to be unified and a unifier $\theta$.


Output: $\theta$, a unifier that unifies $X$ and $Y$ or raises FAIL exception.


Example: unify( $f(P,P,Q)$, $f(Q,R,a)$ ) = $\{P/a,Q/a,R/a\}$.



unify(X,Y,𝜃) = 
 X = X𝜃
 Y = Y𝜃
 case 
  X is a variable that does not occur in Y:
   return (𝜃{X/Y} ∪ {X/Y}) /*replace X with Y in the substitution terms of 𝜃 add X/Y to 𝜃*/
  Y is a variable that does not occur in X:
   return (𝜃{Y/X} ∪ {Y/X}) /*replace Y with X in the substitution terms of 𝜃 add Y/X to 𝜃*/
  X and Y are indentical constants or variables:
   return 𝜃



  X is f(X1,...,Xn) and Y is f(Y1,...,Yn):
   return (fold_left (fun 𝜃 (X,Y) -> unify(X,Y,𝜃)) 
               𝜃 [(X1,Y1),...,(Xn,Yn)])
  otherwise:
   raise FAIL
}



let unify(X,Y) = unify(X,Y,ϵ)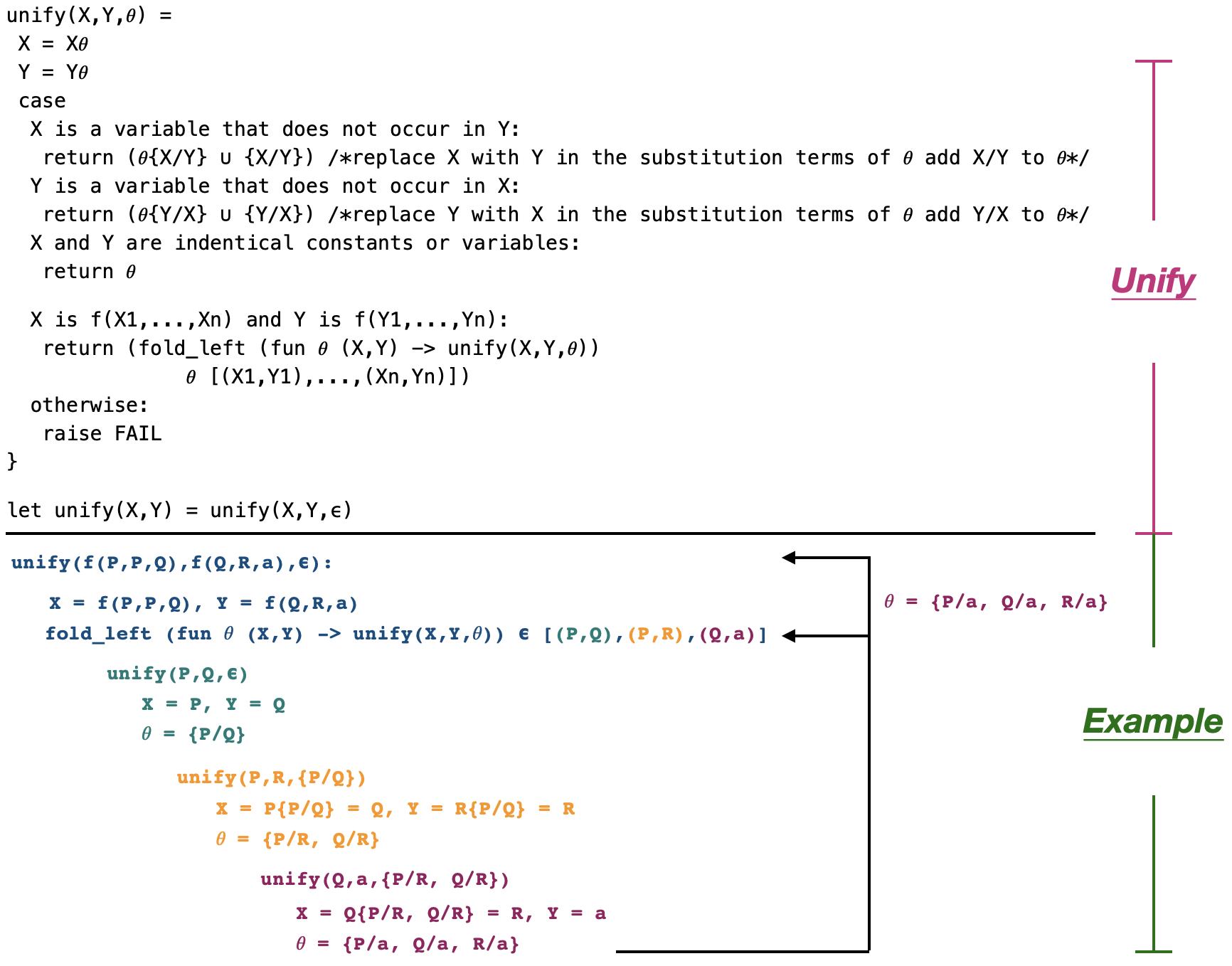
































Abstract interpreter
    

  • Input: A goal Goal and a program P
    

    • 

  • Output: An instance of Goal that is a logical consequence of P.
    

    • 

  • Resolvent (a list) used for maintaining goals or subgoals that the interpreter needs to solve.
    

    • 




















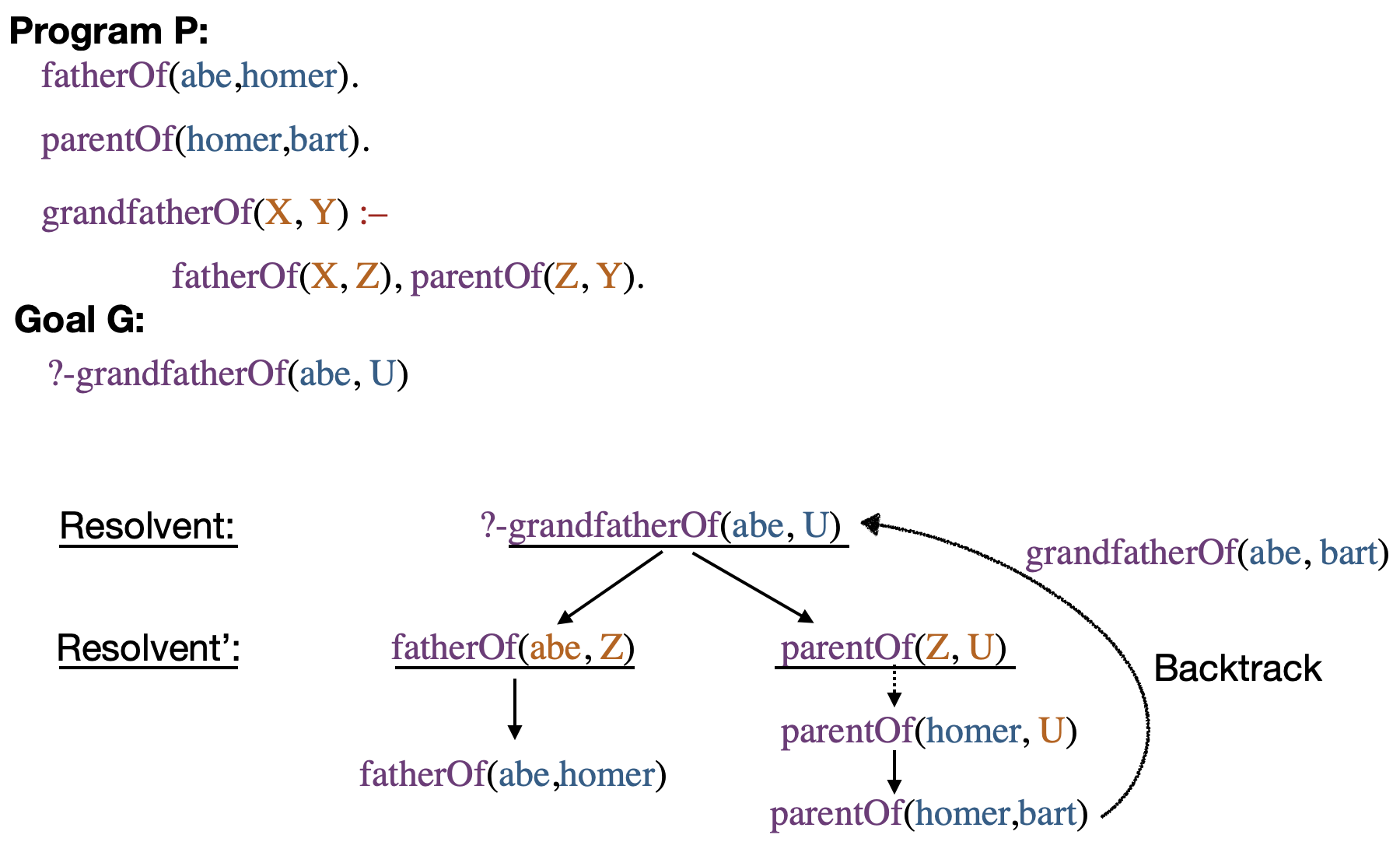
Abstract interpreter
Input: A goal Goal and a program P


Output: An instance of Goal that is a logical consequence of P.


Algorithm: run(P,Goal)



L: G = Goal
   Initialise resolvent to G.
   while (the resolvent is not empty) {
      choose a goal A from the resolvent //random goal
      choose a (renamed) clause A' <- B1,...,Bn from P 
        such that A and A' unify with a unifier 𝜃 // random rule
      (if no such goal and clause exist, exit the while loop).
      replace A by B1,...,Bn in the resolvent
      apply 𝜃 to the resolvent and G 
   }
   If the resolvent is empty, then output G, else goto L.















    

  • In the code, renaming freshens a clause (or a term) by returning a new clause (or a new term) where the clause (or term) variables have been renamed with fresh variables.
    • 

  • We may need to apply a rule multiple times in the nested loop. Keep a rule refreshed before using avoids naming confliction.
    • 

































Abstract interpreter is non-deterministic
    

  • Observe that the abstract interpreter deliberately does not encode the rule and goal order explicitly.
      

    • Nor does it encode what happens on failure to prove a goal (no backtracking).
      • 

    • How does it work then?
      • 

    

    • 
















Abstract interpreter is non-deterministic
Consider the program:



plus(1,3,4).
plus(2,2,4).
even(2).


and the goal plus(X,Y,4), even(X).


    

  • Both plus(2,2,4) and plus(1,3,4) unify with plus(X,Y,4). 
    • 

  • But only plus(2,2,4) ensures that the second goal even(X) is satisfied. 
    • 

  • Since the abstract interpreter in non-deterministic, one of its behaviours is to choose plus(2,2,4), which will lead to success without failure.
    • 
















Abstract interpreter is non-deterministic
Consider the program:



plus(1,3,4).
plus(2,2,4).
even(2).
odd(1).


and the goal plus(X,Y,4), even(X).


OTOH, if the second goal even(X) is chosen as the first to resolve, then it will only unify with even(2), which will change the other goal to plus(2,Y,4) which leaves only one choice.


Non-determinism is essential for correctness.















Backtracking and choice points
    

  • The abstract interpreter does not explicitly encode backtracking (recover from bad choices) and choice points (present more than one result).
    • 

  • SWI-Prolog is deterministic.
      

    • Backtracking and choice points are necessary. 
      • 

    

    • 
















Backtracking and choice points
    

  • Backtracking and choicepoints are encoded more naturally in a recursive formulation of the abstract interpreter.
      

    • Left as a task to you in the final project.
      • 

    

    • 




















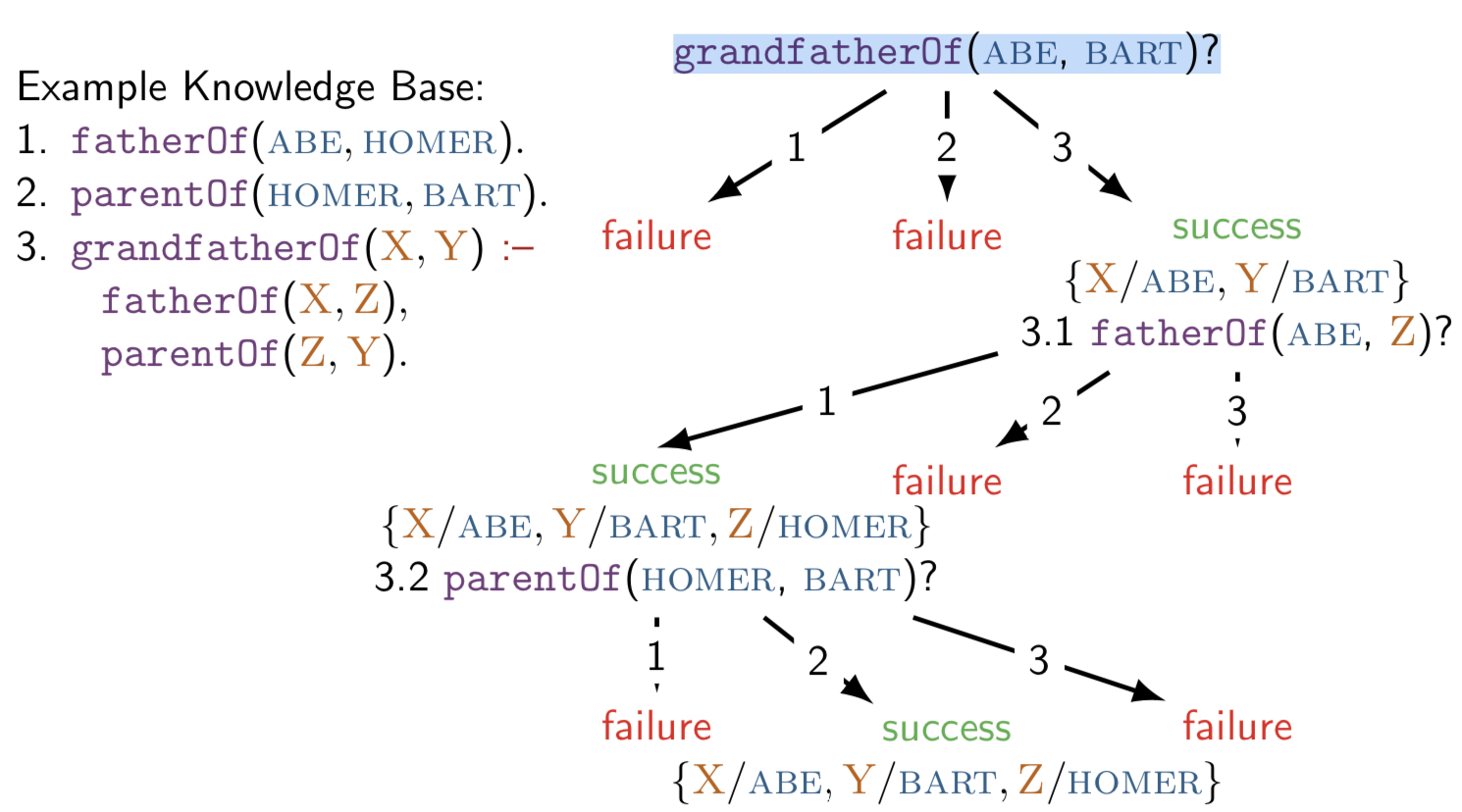
Quiz
Which of these unify?


    

  1. tree(l,r) & tree(B,C) yes
    2. 

  2. tree(A,r) & tree(l,C) yes
    3. 

  3. tree(A,r) & tree(A,B) yes
    4. 

  4. A & a(A) yes (mostly), occurs check disabled by default
    5. 

  5. a & a(A) no
    6. 



















 Occurs check problem. 
















Occurs check problem
Consider the query













In [1]:



    


append([],Q,Q).
append([H | P], Q, [H | R]) :- append(P, Q, R).



    















    






Added 2 clauses(s).


















In [ ]:



    


?- append([],E,[a,b|E]).



    















goes down an infinite search path.


Exercise: Trace by hand to verify why.















Occurs check problem
Consider the query



?- append([],E,[a,b | E]).


    

  • In order to unify this with, append([],Q,Q), we will unify E = [a,b | E], whose solution is E = [a,b,a,b,a,b,...].
    • 

  • In the name of efficiency, most prolog implementations do not check whether E appears on the RHS term.
      

    • infinite loop on unification. 
      • 

    

    • 
















Occurs check problem
You can explicitly turn on occurs check in SWI Prolog.













In [2]:



    


?- set_prolog_flag(occurs_check,true).



    















    






true.


















In [3]:



    


?- append([],E,[a,b | E]).



    















    






false.




















Occurs check problem
You can explicitly turn occurs check in SWI Prolog to an error.













In [4]:



    


?- set_prolog_flag(occurs_check,error).



    















    






true.


















In [5]:



    


?- append([],E,[a,b | E]).



    















    






ERROR: Caused by: '  append([],E,[a,b | E])'. Returned: 'error(occurs_check(_1654, [Atom('282629'), Atom('222853')]), context(/(append, 3), _1674))'.