Prolog Basics

CS314

Review

Previously

  • Functional Programming in OCaml

Today

  • Introduction to Logic Programming in Prolog

Imperative programming

Computing the sum of the elements of an integer list in Java.

int sum (int[] list) {
    int result = 0;
    for (int i = 0; i < list.length; i++)
        result += list[i];
    return result;
}

Functional Programming

Computing the sum of the elements of an integer list in OCaml.

let rec sum l = match l with
  | [] -> 0
  | x::xs -> x + sum xs

Logic Programming

Computing the sum of the elements of an integer list in Prolog.

In [12]:
sum([],0).
sum([H | T], N) :- sum(T,M), N is H+M.





















Notice that this is a declarative reading of the sum of a list.















Declarative vs Operational
    

  • This Prolog program says what the sum of a list is.
      

    • OCaml and Java programs were about how to compute the sum.
      • 

    

    • 

  • In particular, prolog program does not define control flow through the program.
      

    • program is a collection of facts and rules
      • 

    

    • 
















Prolog Program Answers Questions


            +-----------------+
Queries ==> |  Facts + Rules  | ==> Answers
            +-----------------+
               Prolog Program


Facts and rules together build up a database of relations.















Relational view of the sum program
The program


sum([],0)
sum([H | T], N) :- sum(T,M), N is M+H



inductively defines a table of relations:



+-------------+
| List  | Sum |
|-------|-----|
| []    | 0   |
| [1]   | 1   |
| [1,2] | 3   |
| [2]   | 2   |
| ...   | ... |















Queries are look ups in this table












In [13]:



    


?- sum([1,2,3],X).



    















    






X = 6 .




















Of course, the computation model is not to build a database and look up facts.















Why this declarative view?
    

  • Many problems in computer science are naturally expressed as declarative programs.
      

    • Rule-based AI, Program Analysis (asking questions on code), Type Inference, queries on graphical programs, UIs.
      • 

    

    • 

  • But the programmer has to convert this to Von Neumann Architecture. 
    • 





















Logic Programming to the rescue
    

  • Logic programming the programmer to declaratively express the program
    • 

  • The compiler will figure out how to compute the answers to the queries. 
    • 




  Prolog = Logic (programmer) + Control (compiler)















Prolog
    

  • Is one of the first logic programming languagues
      

    • to be precise, it is a family of languages that differ by the choice of control
      • 

    

    • 

  • Invented in 1972, and has many different implementations
    • 
















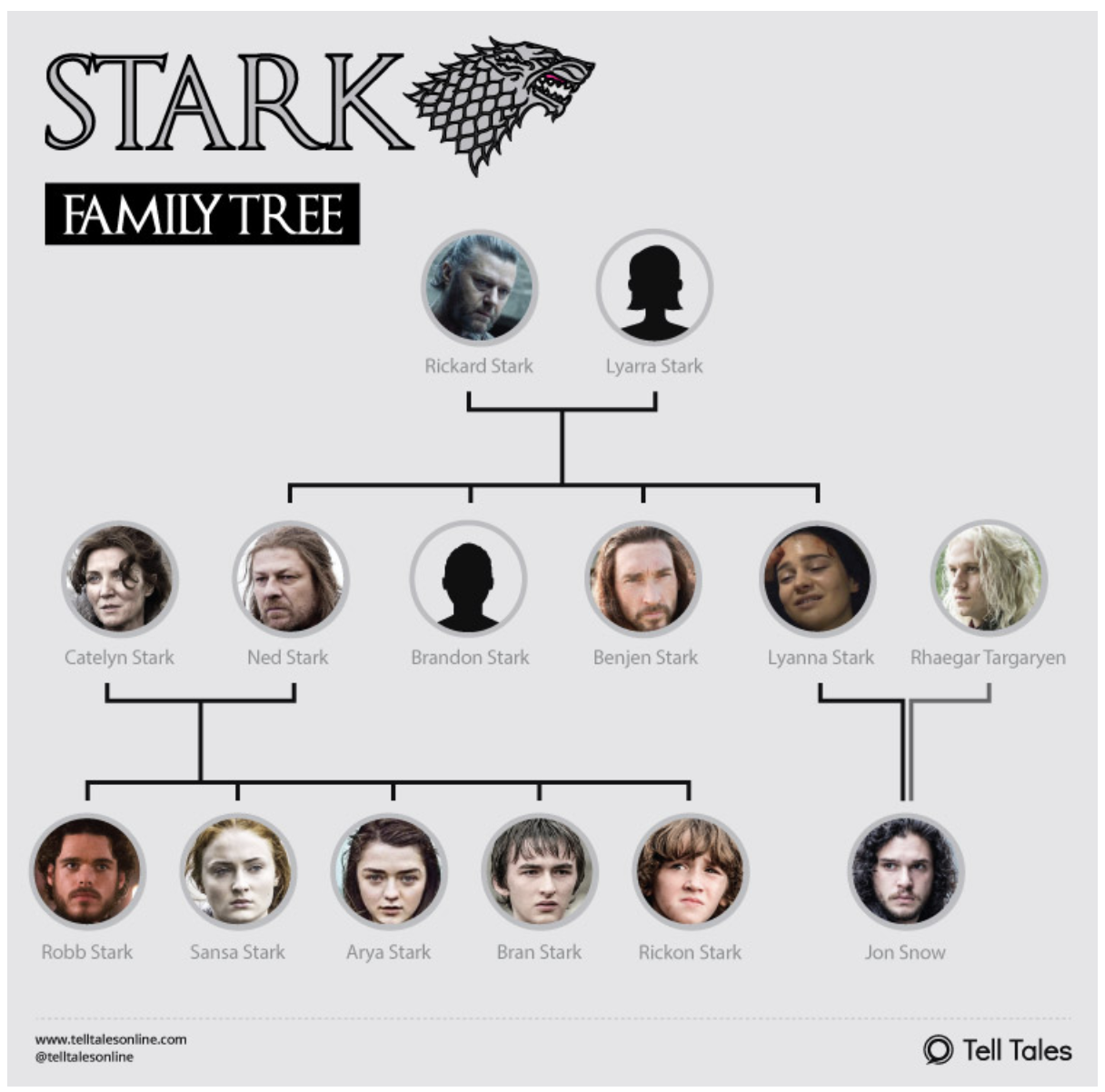
House Stark


















Prolog Terms
Prolog programs are made up of terms.


    

  • Constants: 1,2,3.14,robb,'House Stark', etc. 
      

    • also known as atoms.
      • 

    

    • 

  • Variables: Always begin with a capital letter.
      

    • X, Y, Sticks, _.
      • 

    

    • 

  • compound terms: male(robb), father(ned,robb).
      

    • Top-function symbol/functor: male, father
      • 

    • arity: Number of arguments; male = 1, father = 2.
        

      • top function symbols also written down explicitly with arity such as male/1, father/2.
        • 

      

      • 

    

    • 
















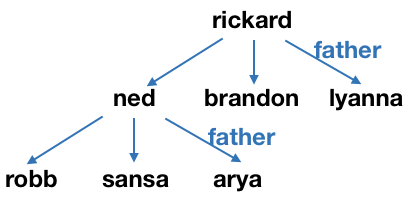
House Stark -- Facts












In [14]:



    


father(rickard,ned).
father(rickard,brandon).
father(rickard,lyanna).
father(ned,robb).
father(ned,sansa).
father(ned,arya).



    















    












































House Start -- Queries












In [15]:



    


?- father(ned,sansa).



    















    






true.


















In [16]:



    


?- father(rickard,sansa).



    















    






false.






































Closed world assumption
We know that Ned is the father of Bran.


Let us query our program.













In [17]:



    


?- father(ned,bran).



    















    






false.




















    

  • Closed World Assumption: Prolog only knows the fact that it has been told.
    • 

  • Assumes false for everything else.
    • 

  • Interesting interactions with negation (we will see this later).
    • 




















Existential Queries
    

  • Apart from true/false questions, we can also ask queries that return other answers (existential queries).
    • 



"Who are Ned's children?"













In [18]:



    


?- father(ned, X).



    















    






X = robb ;
X = sansa ;
X = arya .






































Existential Queries














"Who is the father of Arya?"













In [19]:



    


?- father(X,arya).



    















    






X = ned .




















"Who are Robb's children?"













In [20]:



    


?- father(robb,X).



    















    






false.






































Rules
    

  • So far what we have done could have been done with a relational database.
    • 

  • Rules define further facts inductively from other facts and rules.
    • 

  • Rules have a head and body.
      

    • H :- B1, B2, B3, ..., BN
      • 

    • $H$ is true if $B1 \wedge B2 \wedge B3 \ldots BN$ is true. 
      • 

    

    • 
















Rules












In [21]:



    


parent(X,Y) :- father(X,Y).

ancestor(X,Y) :- parent(X,Y).
ancestor(X,Y) :- parent(X,Z), ancestor(Z,Y).



    















    


























Observe that Z only appears on the RHS of the last rule.















Rules












In [22]:



    


?- ancestor(rickard,X).



    















    






X = ned ;
X = brandon ;
X = lyanna ;
X = robb ;
X = sansa ;
X = arya .




















parent(X,Y) :- father(X,Y).


ancestor(X,Y) :- parent(X,Y).


ancestor(X,Y) :- parent(X,Z), ancestor(Z,Y).




















Exercise
Define mother, cousin, uncle, aunt, sibling.















Example












In [23]:



    


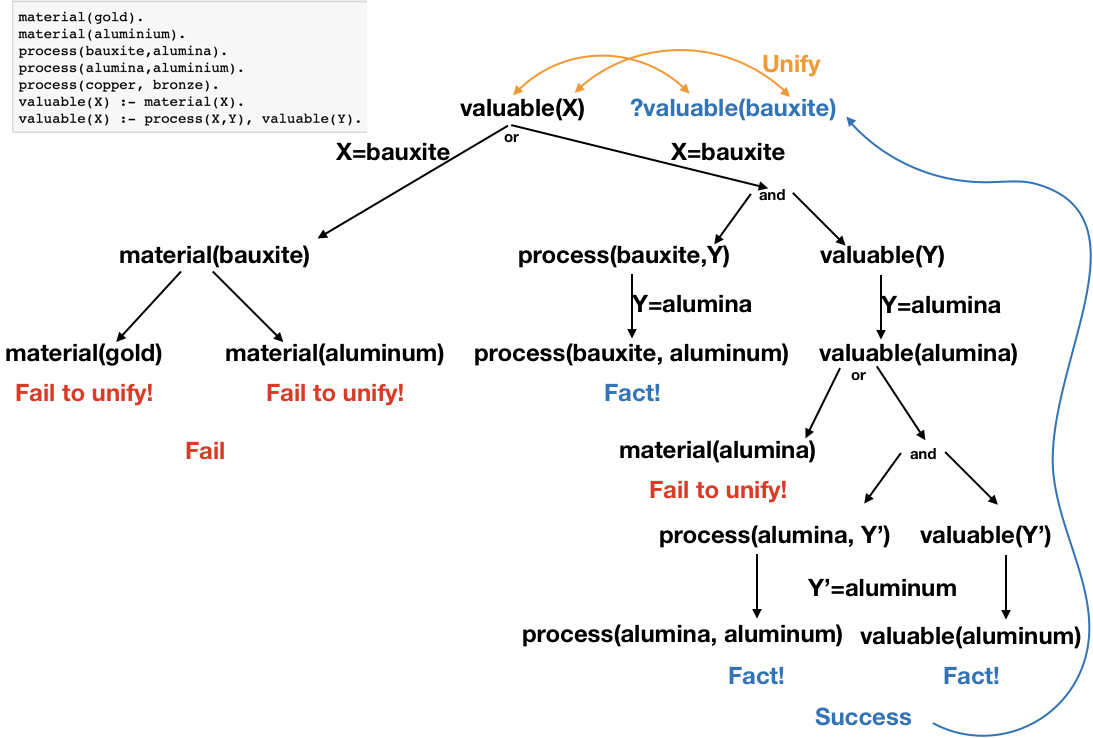
material(gold).
material(aluminium).
process(bauxite,alumina).
process(alumina,aluminium).
process(copper, bronze).
valuable(X) :- material(X).
valuable(X) :- process(X,Y), valuable(Y).



    















    






Added 7 clauses(s).




















    

  • Which of these are valuable? 
      

    • gold, bauxite, bronze, copper.
      • 

    • ?- valuable(gold).
      • 

    • ?- valuable(bauxite).
      • 

    • ?- valuable(bronze).
      • 

    • ?- valuable(copper).
      • 

    

    • 


































Example












In [24]:



    


?- valuable(gold).
?- valuable(bauxite).
?- valuable(bronze).
?- valuable(copper).



    















    






true.
true.
false.
false.




















Unification
At the core of how Prolog computes is Unification.


There are 3 rules for unification:


    

  • Atoms unify if they are identical
      

    • e.g., bauxite & bauxite unifty but not bauxite & gold.
      • 

    

    • 

  • Variables unify with anything.
      

    • e.g., X & bauxite unify, X & valuable (bauxite).
      • 

    

    • 

  • Compound terms unfiy only if their top-function symbols and arities match and their arguments unify recursively.
      

    • e.g., valuable(X) & valuable(baxite) unify, process(bauxite, Y) & process(bauxite, alumina) unify.
      • 

    

    • 
















Quiz
Which of these unify?


A. a & a

B. a & b

C. a & A

D. tree(l,r) & A















Quiz
Which of these unify?


A. a & a yes

B. a & b no

C. a & A yes

D. tree(l,r) & A yes















Quiz
Which of these unify?


A. tree(l,r) & tree(B,C)

B. tree(A,r) & tree(l,C)

C. A & a(A)

D. a & a(A)















Quiz
Which of these unify?


A. tree(l,r) & tree(B,C) yes

B. tree(A,r) & tree(l,C) yes

C. A & a(A) yes (mostly), occurs check disabled by default

D. a & a(A) no