Important notes about grading:¶
- Compiler errors: Programs that cannot be compiled will receive an automatic zero. If you are having trouble getting your assignment to compile, please visit recitation or office hours.
- Late assignments: Please carefully review the course website's policy on late assignments, as all assignments handed in after the deadline will be considered late. Submitting an incorrect version before the deadline and realizing that you have done so after the deadline will be counted as a late submission.
Compile and run your code:¶
After downloading and unzipping the file for assignment3, in your command-line window, cd into the directory which contains src. You should write your code in src/assignment3.ml and src/eval.ml.
Use make to compile the code. Then, use ./imp to excute it.
Submission:¶
Please submit to Sakai with a zip file including assignment3.ml and eval.ml only.
Library functions:¶
You can use any library functions in the List module for this assignment (please do not use library functions in any other modules). You may find the following functions particularly useful, e.g., List.mapi, List.mem_assoc, and List.assoc.
Datatypes:¶
Problems 1-3 are about manipulating tree data structures.
In OCaml, you can define a tree data structure using datatype:
type 'a tree = Leaf | Node of 'a tree * 'a * 'a tree
We will assume binary search trees in this assignment and can define a bineary search tree insertion function as the following:
let rec insert tree x =
match tree with
| Leaf -> Node(Leaf, x, Leaf)
| Node(l, y, r) ->
if x = y then tree
else if x < y then Node(insert l x, y, r)
else Node(l, y, insert r x)
We can construct a binary search tree from a list:
let construct l =
List.fold_left (fun acc x -> insert acc x) Leaf l
Problem 1¶
We have seen the benefits of the 'fold' function for list data structures. In a similar fashion, write a function
fold_inorder : ('a -> 'b -> 'a) -> 'a -> 'b tree -> 'a
That does a inorder fold of the tree. For example,
fold_inorder (fun acc x -> acc @ [x]) [] (Node (Node (Leaf,1,Leaf), 2, Node (Leaf,3,Leaf))) = [1;2;3]
let rec fold_inorder f acc t =
(* YOUR CODE HERE *)
assert (fold_inorder (fun acc x -> acc @ [x]) [] (Node (Node (Leaf,1,Leaf), 2, Node (Leaf,3,Leaf))) = [1;2;3]);
assert (fold_inorder (fun acc x -> acc + x) 0 (Node (Node (Leaf,1,Leaf), 2, Node (Leaf,3,Leaf))) = 6)
Problem 2¶
Given a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
levelOrder : 'a tree -> 'a list list
Example:
Given a tree t: 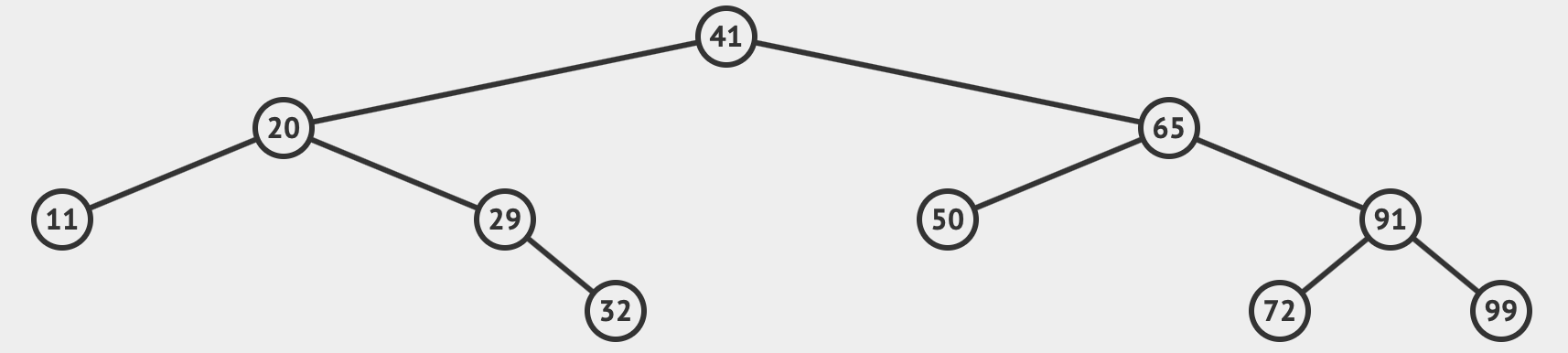
the returned result of levelOrder t should be a nested list [[41];[20;65];[11;29;50;91];[32;72;99]]. The ith elment of the nested list is a list of tree elements at the ith level of the tree t from left to right. You may need to define a recursive auxiliary function.
Note: OCaml queues are mutable first-in-first-out (FIFO) data structures, and hence are not functional. Since our goal is to practice functional programming, please do not use OCaml queues for this assignment.
let levelOrder t =
(* YOUR CODE HERE *)
Problem 3¶
The usual recursive formulation of the function that computes the sum of a tree
let rec sum_tree t =
match t with
| Leaf -> 0
| Node (l, x, r) -> sum_tree l + x + sum_tree r
is not tail-recursive.
For a tail recursive implementation, you may need to use an auxiliary function of type
aux: int -> int tree list -> int
Hint: aux acc ts takes as input an accumulator acc as usual and a list of sub-trees obtained from the input tree. The idea is that when the list is empty, acc is the sum of all input-tree elements. Implement a tail recursive function sumtailrec that uses this idea.
sumtailrec: int tree -> int
Your solution must be strictly tail-recursive. The following solution sums all nodes on the left branch l and then all nodes on the right branch r is incorrect. Calling the aux function twice in the recursive code makes the function not tail-recursive because you need a stack frame for the first call. You should only call the aux function once in the recursive code. Following the hint above can correct this solution.
let rec aux (acc:int) (ts: int tree) =
match ts with
| Leaf -> acc
| Node(l, x, r) -> (aux (aux (acc+x) l)) r
let sumtailrec t =
(* YOUR CODE HERE *)
let tree = construct [2;1;3] in
assert (sumtailrec tree = sum_tree tree)
Operational Semantics¶
Problem 4¶
In this problem, you will implement a definitional interpreter (aka an evaluator) for Imp, an imperative language. The language contains variables, integer and boolean types, equality and comparison operations, math and boolean operations, and simple control flow.
Recall from class that a definitional interpreter is a function that takes a program's abstract syntax tree (AST) and evaluates it to its final result. For Imp, this final result is an environment, which is a map from variables to their (current) values. Imp's AST is defined by the type com (commands), and environments are defined by the type environment in the file ast.ml. Your job will be to implement the function
eval_command : com -> environment -> environment
which will evaluate the given command (first argument) starting with the given environment (second argument), producing the final environment. Since commands also include (arithmetic and other) expressions, you will also implement the function
eval_expr : exp -> environment -> value
This function evalutes the given expression to its final value in the given environment. Both of your functions will go in the file eval.ml; you should not modify any other files that are given to you.
ast.ml: Abstract Syntax Trees, Environments, Values¶
As mentioned above, the Imp AST is defined by the type com in ast.ml. This type has the following definition:
type com =
| While of exp * com
| For of exp * com
| Cond of exp * com * com
| Comp of com * com
| Assg of string * exp
| Declare of dtype * string
| Print of exp
| Skip
Each part of this datatype corresponds to a kind of Imp command. For example, Skip is an empty command. Assg of string * exp corresponds to an assignment command, where the string part indicates a variable name, and the exp part indicates the expression whose value should be assigned to the variable. Comp of com * com is a command that is itself a pair of other commands, with the first executed before the second. We explain this AST in detail in the next section. Note that the types exp and dtype are part of the Imp AST, too; they are referenced in com's definition above.
In a full-fledged interpreter, a parser is used to convert a normal text file into its corresponding AST. In this project, we provide a parser for you. For example, consider the following input file:
int n;
int f;
n := 5;
f := 1;
while (n > 1) {
f := f * n;
n := n - 1;
};
The parser will take this and produce the following com:
Comp(Declare (Int_Type, "n"),
Comp(Declare (Int_Type, "f"),
Comp (Assg ("n", Number 5),
Comp (Assg ("f", Number 1),
While (LT (Number 1, Var "n"),
Comp(Assg ("f", Times (Var "f", Var "n")),
Assg ("n", Minus (Var "n", Number 1))))))))
This com uses Comp to string together each of the commands in the file, one for each line. The Declare(Int_Type, "n") part corresponds to the first line int n. The Assg("n", Number 5) corresponds to the third line n := 5. And so on.
We suggest before coding you look at the Imp input examples in /programs. You should be able to get a sense of how these examples correspond to the com type above.
Also in ast.ml are the definitions of type value and environment. The former is the result from evaluating an expression (i.e., something of type exp). The latter is a map from variables to values; it keeps track of the current value assigned to a given variable. Here are their definitions:
type value =
| Int_Val of int
| Bool_Val of bool
type environment = (string * value) list
A value (the result of evaluating an expression) is either an integer or a boolean. An environment is a list of pairs, where the first element is a variable name and the second is its current value. This representation is called an association list - the first element of the pair is associated with the second. Elements earlier in the list override elements later in the list. The List module has many useful functions for working with association lists which you should consider using in your implementation.
eval.ml: The Evaluator¶
To implement the definitional interpreter (i.e., the evaluator) you must implement two functions, eval_expr and eval_com in the file eval.ml. This is the only file you should modify.
eval_com : com -> environment -> environment
eval_expr : exp -> environment -> value
Each of these takes as an argument an environment. Evaluating a command might modify an environment (e.g., due to a variable assignment), so eval_com produces an environment as output. Evaluating an expression will never change the environment, and so eval_expr only produces the final value. Both take an environment as input in which the evaluator can look up current values of variables.
To see these functions in action, to give you a sense of what they do, consider some elements from our example Imp program above.
First, consider Declare (Int_Type, "n"), a com that represents an Imp command. If we evaluate it in an empty environment [], we should get an output environment [("n", Int_Val 0)]. That is,
eval_com [] (Declare (Int_Type, "n")) = [("n", Int_Val 0)]
An integer variable is initialized to 0 by the interpreter.
Now, consider Assgn("n", Number 5), a com that represents an Imp command. We evaluate it in an environment [("f", Int_Val 0); ("n", Int_Val 0)]. We will get an output environment where we have n mapped to Int_Val 5. That is,
eval_com (Assign("n", Number 5)) [("f", Int_Val 0); ("n", Int_Val 0)] = [("n",Int_Val 5); ("f", Int_Val 0); ("n", Int_Val 0)]
Now consider LT (Number 1, Var "n"), an exp that represents an Imp expression. Evaluating it in the environment produced above, we would have
eval_expr (LT (Number 1, Var "n")) [("n", Int_Val 5); ("f", Int_Val 0); ("n", Int_Val 0)] = Bool_Val true
i.e., n = 5 is indeed greater than 1.
In what follows, we will step through each of the variants of the exp and com types to say what your interpreter should do with them.
The interpreter concerns error cases as well such as addition between a boolean and an integer and therefore represent a stuck reduction. The expected behavior for these irreducible error cases can be boiled down to the following rules:
- Any expression containing division by zero should raise a
DivByZeroerror when evaluated. - Any expression or command that is applied to the wrong types should raise a
TypeErrorexception when evaluated, for example, the expression 1 + true would result inTypeError. - An expression or command that assigns to an undefined variable, or reads from an undefined variable should raise a
UndefinedVarwhen evaluated. - The above exceptions are defiend in
eval.ml. Evaluation of subexpressions should be done from left to right in order to ensure that lines with multiple possible errors match up with our expected errors.
Function 1: eval_expr¶
eval_expr takes an expression e and an environment env, and it produces the result of evaluating e, which is something of type value (Int_Val or Bool_Val). Here's what to do with each element of the expr type:
Number
Integer literals evaluate to a Int_Val of the same value.
True, False
Boolean literals evaluate to a Bool_Val of the same value.
Var
An identifier (variable) evaluates to whatever value it is mapped to by the environment. Should raise a UndefinedVar if the identifier has no binding.
Plus, Minus, Times, Div, and Mod
These mathematical operations operate only on integers and produce a Int_Val containing the result of the operation. All operators must work for all possible integer values, positive or negative, except for division, which will raise a DivByZeroError exception on an attempt to divide by zero. If either argument to one of these operators evaluates to a non-integer, a TypeError should be raised.
Or and And
These logical operations operate only on booleans and produce a Bool_Val containing the result of the operation. If either argument to one of these operators evaluates to a non-boolean, a TypeError should be raised.
Not
The unary not operator operates only on booleans and produces a Bool_Val containing the negated value of the contained expression. If the expression in the Not is not a boolean (and does not evaluate to a boolean), a TypeError should be raised.
Less (Lt), LessEqual (Leq)
These relational operators operate only on integers and produce a Bool_Val containing the result of the operation. If either argument to one of these operators evaluates to a non-integer, a TypeError should be raised.
Equal (Eq)
The equality operator operates both on integers and booleans, but both subexpressions must be of the same type. The operators produce a Bool_Val containing the result of the operation. If the two arguments to the operator do not evaluate to the same type (i.e. one boolean and one integer), a TypeError should be raised.
Function 2: eval_com¶
eval_com takes a command c and an environment env and produces an updated environment (defined in Types) as a result.
Skip
Skip is short for "no operation" and should do just that - nothing at all. The environment should be returned unchanged when evaluating a Skip.
Comp
The Comp sequencing command is used to compose whole programs as a series of commands. When evaluating Comp, evaluate the first subcommand under the environment env to create an updated environment env'. Then, evaluate the second subcommand under env', returning the resulting environment.
Declare
The Declare command is used to create new variables in the environment. If the type being declared is Int_Type, a new binding to the value Int_Val(0) should be made in the environment. If the type being declared is Bool_Type, a new binding to the value Bool_Val(false) should be made in the environment. The updated environment should be returned.
Assg
The Assg command assigns new values to already-declared variables. If the variable hasn't been declared before assignment, a UndefinedVar should be raised. If the variable has been declared to a different type than the one being assigned into it, a TypeError should be raised. Otherwise, the environment should be updated to reflect the new value of the given variable, and an updated environment should be returned.
Cond
The Cond command consists of three components - a guard expression, an if-body command and an else-body command. The guard expression must evaluate to a boolean - if it does not, a TypeError should be raised. If it evaluates to true, the if-body should be evaluated. Otherwise, the else-body should be evaluated instead. The environment resulting from evaluating the correct body should be returned.
While
The While command consists of two components - a guard expression and a body command. The guard expression must evaluate to a boolean - if it does not, a TypeError should be raised. If it evaluates to true, the body should be evaluated to produce a new environment and the entire loop should then be evaluated again under this new environment, returning the environment produced by the reevaluation. If the guard evaluates to false, the current environment should simply be returned.
For
The For loop command consists of two components - a guard expression and a body command. Upon entering the loop, the guard expression a is evaluated in the current environment, yielding an integer n. If the int value n is 0, the loop body is not executed at all. If n is greater than 0, then the loop body is executed n times. No action in the body of the loop, such as assigning to a variable, can change the number of times the loop is executed, nor does executing the body alone change the value of any variable except by explicit assignment.
Parser¶
A real interpreter has two parts: a parser, which takes text files and converts them into an AST, and an evaluator, which runs the AST to produce a final result. Your job has been to implement the evaluator. To help you test this evaluator, we are providing code that will do parsing for you. The function load in assignment3.ml will take in a text file and produce an AST of type com. Our parser (called in load) expects an input file whose contents is a command (or a sequence of commands, which will be parsed as a single Comp). We suggest before coding you look at the Imp input examples in /programs. You should be able to get a sense of how these examples correspond to the com type above. Our code in the function eval in assignment3.ml passes the parsed AST to your eval_command function with an empty environment.
In the following example, we parse a program from file and apply the eval function to obtain the evaluation result of the loaded program. We use a given function print_env_str to convert the output environment to string (after removing shadowed variables in the environment). The program is:
int x;
int y;
x := 5;
x := x + 5;
y := 5 + 5;
y := 5 + x;
Obviously, after evaluation, x = 10 and y = 15.
let parsed_ast = load ("programs/aexp-add.imp") in
let result = print_env_str(eval (parsed_ast)) in
assert(result =
"- x => 10\n\
- y => 15\n")
One thing you may need to pay attention to for programming the interpreter is nested pattern matching. You will need parentheses to clearly delimit scoping, e.g.,
match e with
| Plus (e1, e2) ->
let r1 = eval_expr e1 env in
let r2 = eval_expr e2 env in
(match r1, r2 with
| Int_Val i, Int_Val j -> ...
| _ -> ...) (* The parentheses are needed to delimit the scope of the two pattern-matchings *)
| Minus (e1, e2) -> ...